

| 2 Morpho-Phonology | 7a Using Affixes | 12 The Number System | |
| 3 Basic Morphology | 7b Using Affixes (continued) | The Lexicon | |
| 4 Case Morphology | 8 Adjuncts | Revised Ithkuil: Ilaksh |
| 12.1 Features of a Centesimal Number System |
| 12.2 Semantic Designations for Numerical Stems |
| 12.3 Expressing Zero |
| 12.4 Writing Numerals |
| 12.5 Using Numbers in Speech |
The Ithkuil system of numbers and counting is distinct from Western languages in two fundamental ways: it is centesimal (base one hundred) as opposed to decimal (base ten), and the numbers themselves are full formatives (i.e., nouns and verbs), not adjectives. This has already been discussed briefly in Section 4.5.7 regarding the PARTITIVE case. This section will examine the numerical system in greater detail.
Being a centesimal system of enumeration, the numbers from zero to 100 are considered autonomous units represented by single stems and written using single autonomous symbols. Beginning with the number 101, numbers are referred to by the number of hundreds plus the number of units, just as a decimal system, beginning with the number 11, refers to the number of tens plus the number of units. However, where a decimal system then shifts to a unit referring to 100 once 10 tens is reached, a centesimal system proceeds to the number 10,000 before establishing a new unit reference (i.e., 100 hundreds). Thus the number 3254, which in a decimal system is 3 thousands 2 hundreds 5 tens 4 ones, in a centesimal system becomes 32 hundreds54 ones, and would be only two digits when written (the single character representing 32, and the single character representing 54). The details of writing Ithkuil numerals are given below in Section 12.5.
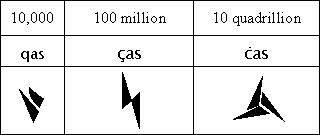
After 100, separate unit numbers and symbols are assigned to
the square of 100 (i.e. ten thousand, that being 100 hundreds),
then the square of that number, ![]() (100 million, i.e., 10,000 ten-thousands). The final unit is
(100 million, i.e., 10,000 ten-thousands). The final unit is ![]() ,
that is, 10 quadrillion or 100 million hundred-millions, the last number for
which Ithkuil assigns a separate root and symbol. After ten quadrillion, numbers
are referred to as multiples of lower sets, similar to saying in English one
trillion quadrillion instead of the equivalent one octillion.
,
that is, 10 quadrillion or 100 million hundred-millions, the last number for
which Ithkuil assigns a separate root and symbol. After ten quadrillion, numbers
are referred to as multiples of lower sets, similar to saying in English one
trillion quadrillion instead of the equivalent one octillion.
While the above may seem unwieldy or even arbitrary, it actually
parallels Western base-ten numerals in terms of its systematization. For example,
in a Western number like 456,321,777,123, each set of three numbers between
the commas tells how many hundreds there are of a certain power of 1000 (i.e.,
there are 123 of_![]() ,
777 of_
,
777 of_![]() ,
321 of_
,
321 of_![]() ,
and 456 of_
,
and 456 of_![]() ,
or in more common terms 123 ones, 777 thousands, 321 millions, 456 billions).
,
or in more common terms 123 ones, 777 thousands, 321 millions, 456 billions).
The same exact system holds for Ithkuil, except that the sets
of numbers between the commas so to speak, is the number of ten-thousands,
not thousands. Thus, if we were to rewrite the Western number 456,321,777,123
in such a system, it would be 4563,2177,7123 (i.e., 7123 of_![]() ,
2177 of_
,
2177 of_![]() ,
and 4563 of_
,
and 4563 of_![]() ,
that being 7123 ones, 2177 ten-thousands, and 4563 hundred-millions).
,
that being 7123 ones, 2177 ten-thousands, and 4563 hundred-millions).
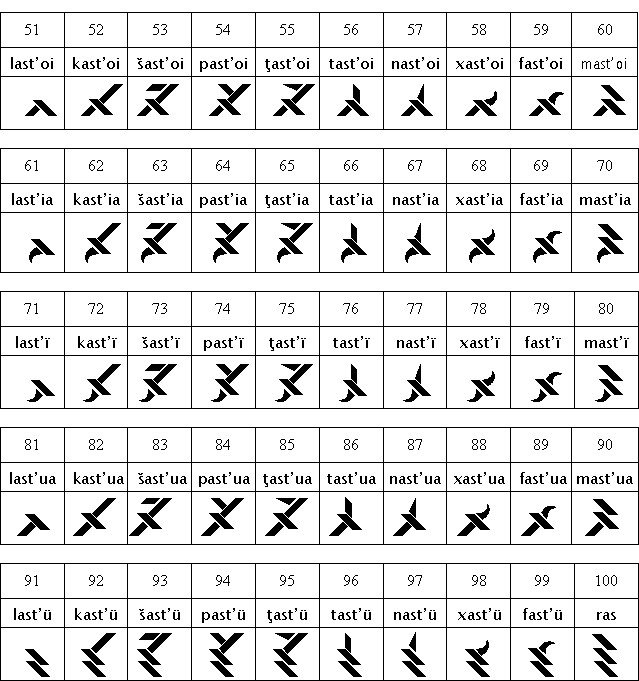
The semantic roots for numbers in Ithkuil from 1 to 99 are
based on roots for 1 through 10, to which the nine degrees of the affix -V1t
are added. Each of the nine degrees of this suffix, when applied to one of the
ten number-roots, corresponds to an additional multiple of ten. This is illustrated
in Table 67 below.
Table 67:
The ![]() Affix with Numerals
Affix with Numerals

The addition of a particular degree of this affix to one of the ten indicates that the root number is added to that multiple of ten. For example, the stem kas two, plus the seventh degree affix -V1t/7, gives kastï seventy-two. Because there is no root corresponding to zero (see Sec. 12.3 below), each multiple of ten is constructed using stem mas ten plus one of the above suffixes. Thus, the numbers 20, 30 and 40 are respectively mast, mastu and mastai, but the numbers 22, 32 and 42 are kastu, kastai and kastei. This pattern only operates up to the nineties, as there is a separate autonomous root for 100, r-s.
Since numbers are formatives in Ithkuil, not adjectives as in most Western languages, holistic stem No. 1, shown by the vocalic infix -a-, is a formative signifying a set containing a number of members corresponding to that particular root. Thus, the formative kas above, translatable as two, actually means a set of two; a duo / to be a duo. In turn, the two complementary derivatives of each stem denote its multiple and its fraction respectively. This is illustrated below for both Form I and II using the roots k-s, TWO, and n-s, meaning SEVEN:
For k-s, TWO:
1. kas/kâs a set of two, a duo; to be two in number
COMPLEMENTARY DERIVATIVES:
kes/kês: twice the number of something; to double, to multiply by two
käs/kaes: a half; to halve, to be or make half, to divide by or in two
2. kus/kûs to be or make dual; having two uses or aspects; bi-; twofold
COMPLEMENTARY DERIVATIVES:
kos/kôs: two times (i.e., iterations), twice; to be/do/make twice
kös/køs: to be of or make into two parts; bifurcate(d)
3. kis/kîs the second one in a sequence; to be or make second (in a sequence)
COMPLEMENTARY DERIVATIVES:
kës/kÿs: to the second power, squared; to square, raise to the 2nd power
küs/kius: to the negative second power, the inverse square; to divide by the square of
For n-s, SEVEN:
1. nas/nâs a set/group of seven, a septet; to be seven in number
COMPLEMENTARY DERIVATIVES:
nes/nês: 7 times the number of something; to multiply by 7; septuple
näs/naes: a seventh; to be or make a 7th part of something, to divide by 7 or into 7 parts
2. nus/nûs to be or make seven-faceted; having 7 uses or aspects; septi-; sevenfold
COMPLEMENTARY DERIVATIVES:
nos/nôs: 7 times (i.e., iterations); to be/do/make 7 times
nös/nøs: to be of or make into 7 parts; separate(d) into 7 parts
3. nis/nîs the seventh one in a sequence; to be or make 7th (in a sequence)
COMPLEMENTARY DERIVATIVES:
nës/nÿs: to the 7th power; to raise to the 7th power
nüs/nius: to the negative 7th power; to divide by the 7th power of
In addition to the above-described roots, there is the root l-s, ONE/UNITY. As this root has no multiples, its semantic designations follow a unique pattern. NOTE: The INFORMAL versus FORMAL distinction in this root (i.e., Form I versus Form II of each stem) distinguishes between a focus on non-duplication/singularity for the INFORMAL, and indivisibility/unity for the FORMAL:
1. las/lâs a single entity; to be one in number
COMPLEMENTARY DERIVATIVES:
les/lês: to be indivisible, whole, a single unit; unitary; to unify
läs/laes: to be (an) individual, a distinct entity in itself; to individualize
2. lus/lûs a lone entity, something alone; an entity in solitude, something/someone isolated; be alone; to isolate; be in solitude
COMPLEMENTARY DERIVATIVES:
los/lôs: something/someone lonely; be or make lonely
lös/løs: something/someone independent, self-sufficient, singular (i.e., without need of, connection to, or dependency on others); be or make independent, self-sufficient, singular
3. lis/lîs something/someone unique, the only one; to be or make unique
COMPLEMENTARY DERIVATIVES:
lës/lÿs: a sole entity, the only one available or able (in terms of sufficiency or applicability to the context)
lüs/lius: something/someone one-of-a-kind, unparalleled, without equal or peer (in terms of uniqueness of characteristics)
The Ithkuil numerical roots as described in the section above are as follows:
l-s |
k-s |
-s |
p-s |
t-s |
n-s |
x-s |
f-s |
m-s |
|
one |
two |
three |
four |
five |
six |
seven |
eight |
nine |
ten |
r-s |
q-s |
ç-s |
c-s |
one hundred |
ten thousand |
one hundred million |
ten quadrillion |
Ithkuil has no word for zero nor is it conceptualized as a numerical category. Instead any appropriate formative may take the affixes -V1ss/1 or -V2ss/1 no amount of or -V3b/1 no at all in terms of degree or extent to create negative expressions that convey the idea of an absence of a numerical entity or quantity. In many cases, simply the negative of whatever formative is under discussion may be used.
As for handling the concept of zero as a null placeholder when writing Ithkuil numbers, this is addressed in Section 12.4 below.
Writing Ithkuil numerals is somewhat similar to writing numbers in Western languages (i.e., Arabic numerals), in that the interpretation of a number as a different power of 100 (analogous to interpreting single Arabic numerals as either ones, tens, hundreds, thousands, etc.) is based on its sequence within the entire number. However, there are two aspects of writing Ithkuil numbers that are quite different from Arabic numbers.:
One must also remember that in terms of left-to-right or up-and-down orientation, numbers follow the boustrophedon mode the same as the Ithkuil script (see Sec. 11.3.2). Similarly to Western languages, small non-compound numbers can be written using either their numerical symbols or written out in script (as in English 12 versus twelve).
The following table gives the Ithkuil numerical symbols along
with their morphological stems:
Table 68: ITHKUIL NUMERICAL
STEMS AND WRITTEN SYMBOLS

Spoken numbers are formed from the above stems using both the PARTITIVE and COMITATIVE cases, as well as using the coordinative affix -V1w/1 (= -iw or -wai). The number of largest base units is shown by placing the base-unit term in the PARTITIVE. If this is then followed by another collection of smaller base units, that number of smaller base units is connected using the COMITATIVE case while the smaller base-unit term is again in the PARTITIVE. Single units (from 1 to 99) are connected by the coordinative affix when they are part of the number of hundreds or higher base-units.
It should be noted that when pronouncing numbers greater than 199, it is normal in Ithkuil to omit the word rawirs (= the PARTITIVE of ras one hundred) referring to the number of hundreds. This is equivalent to the custom in colloquial English of saying three twelve for three hundred (and) twelve. The difference is that in Ithkuil, this omission of the word for hundred is the preferred option, the word rawirs being used only in larger numbers for claritys sake.
These principles are illustrated by the following examples:
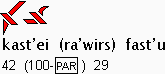
literally: 42 (of hundreds) 29
4229

literally: 26 of ten-thousands with 97 (of hundreds) 66 = 26,9766
269,766
Listen!
![]()
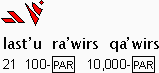
literally: 21 of hundred of ten-thousands
21,000,000
[NOTE: rawirs is required in this example]
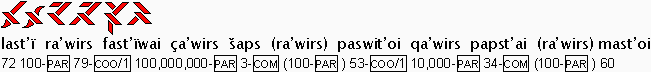
literally:
72 of hundreds and 79 of hundred-millions with 3 of hundreds and 53 of
ten-thousands with 34 of hundreds 60
727,903,533,460
We have already seen that when numbers are used to indicate how many of a certain
noun there are, the noun must appear in the PARTITIVE
case, since the number itself is functioning as the head of the
numerical expression (e.g., English 12 boxes being constructed
in Ithkuil as a 12-set of a box or perhaps more appropriately
a box-dozen). Another syntactical consequences of numbers being
full formatives is when a number functions as a label or overt identifier, as
in the English sentence Youll find him in Room 216. Such usage
of numbers is not primarily sequential (which would involve the equivalent of
ordinal numbers such as fourth, twenty-sixth,
etc. equivalent to stem No. 3 of each number root) but rather organizational
(e.g., as in the three-dimensional array of room numbers in a hotel). Ithkuil
handles such organizational labeling using either the CONTRASTIVE
case (see Sec. 4.5.6) or
the ESSIVE case (see Sec.
4.6.1) depending respectively on whether the enumeration of the noun in
question is to distinguish it from other enumerated nouns versus merely identifying
the noun by a numerical name. Examples:
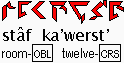
the room marked 12 OR
Room 12 OR Room
No. 12 [i.e., as distinguished from the other numbered rooms]
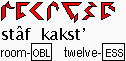
the room marked 12 OR
Room 12 OR Room
No. 12 [identifying reference only]
Lastly, when numbers comprising multiple number-stems are declined for case,
configuration, extension, etc., rather than writing out the entire number long-hand,
the number symbol is used, preceded by the carrier stem kir
(see Sec. 9.4) which carries the appropriate
declensions. This use of the carrier stem applies even to single-stemmed numbers
when writing, in order to allow use of the number symbol instead of writing
it out. In such cases involving single-stemmed numbers, the carrier stem is
not pronounced (rather, the numerical stem bears the pronounced declensions);
it is there only as a written indicator of the declensions to be applied to
the number stem. Thus, the above two examples could also be written as:

| 2 Morpho-Phonology | 7a Using Affixes | 12 The Number System | |
| 3 Basic Morphology | 7b Using Affixes (continued) | The Lexicon | |
| 4 Case Morphology | 8 Adjuncts | Revised Ithkuil: Ilaksh |
©2004-2009 by John Quijada. You may copy or excerpt any portion of the contents of this website provided you give full attribution to the author and this website.